Den här egenskapen uttrycks i ljudabsorptionskoefficienten (α). Ljudabsorptionskoefficienten är förhållandet mellan den ljudenergi som absorberas av materialet (d.v.s. den icke-reflekterade ljudenergin) och den ljudenergi som träffar materialet. Absorptionskoefficienten är därför en faktor mellan 0 och 1, där 0 indikerar att materialet inte absorberar någon ljudenergi alls, medan 1 indikerar att materialet absorberar all ljudenergi. Betong har typiskt en absorptionskoefficient på 0,01-0,02 vilket motsvarar 1-2 %. Troldtekt akustikplattor med mineralull på baksidan har vanligtvis en absorptionskoefficient på 0,8-0,9 vilket motsvarar 80-90 %.
Den ljudabsorberande effekten för ett material i ett visst rum beror naturligtvis inte enbart på storleken på ljudabsorptionskoefficienten, men också på hur många kvadratmeter av materialet som finns i rummet. Absorptionen, även kallad ekvivalent ljudabsorptionsyta (A), är produkten av ytmaterialet multiplicerat med materialets ljudabsorptionskoefficient.
A = S × α (m2 sab)
Måttenheten är metrisk sabin (m2 sab) för att inte förväxla den med en ”normal” yta. Absorptionen uttrycker den totala effekten i rummet av materialet i fråga. Den fysiska innebörden av absorption kan uttryckas som ytan för ett öppet fönster (som absorberar 100 % eftersom ljudet inte kommer tillbaka in i rummet), med samma ljuddämpande effekt som det faktiska antalet kvadratmeter av materialet.
Om vi till exempel tar 10 kvadratmeter Troldtekt med en ljudabsorptionskoefficient på 0,8: Absorptionen är 10×0,8 eller 8 metriska sabiner. Samma effekt kan fås av 8 kvadratmeter öppna fönster som absorberar 100 %. Akustiskt sett, om man monterar 10 kvadratmeter Troldtekt i rummet motsvarar det att ha 8 kvadratmeter öppna fönster. I akustikens barndom användes faktiskt den öppna-fönsterenheten (Open Window Unit, OWU) som en uttryck för absorption, vilket var pedagogiskt.
Vi har nu möjlighet att uttrycka den viktigaste formeln i akustiken, Sabines ekvation, som länkar samman efterklangstiden (T) med rummets volym (V) och absorptionen (A), samt proportionalitetsfaktorn 0,16:
T = 0,16 × V/A, där A = S × α
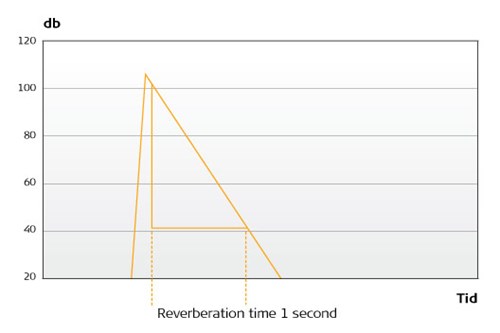
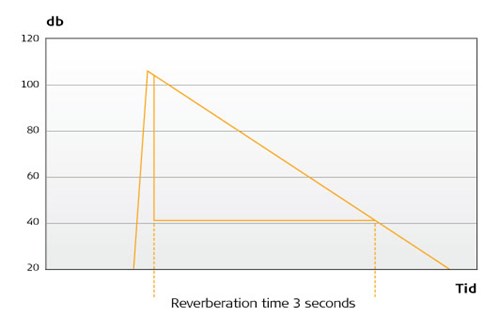
Det viktigaste är att efterklangstiden är proportionell mot volymen av rummet (d.v.s. ett rum med dubbelt så stor volym har dubbelt så lång efterklangstid), och omvänt proportionell mot absorptionen (dubbelt så hög absorption ger halva efterklangstiden). Proportionalitetsfaktorn 0,16 är en konstant som används för att se till att allt stämmer. Som vi vet är efterklangstiden den tid det tar för ljudet att minska med 60 dB. Om en annan definition hade valts – till exempel 40 dB i stället för 60 dB – hade också proportionalitetsfaktorn varit annorlunda.
Sabines efterklangsekvation innebär att det är möjligt att i förväg beräkna den resulterande efterklangstiden när storleken (volymen) på rummet är känd, och när man också vet hur mycket absorption som har tillförts rummet. Redan innan rummet byggts är det därför möjligt att förutsäga den efterklangstid som så småningom kommer att upplevas i det färdiga rummet. För att kunna utföra beräkningen som beskrivits, förutom att veta rummets dimensioner, är det också nödvändigt att känna till de akustiska egenskaperna för de byggmaterial som kommer att användas.
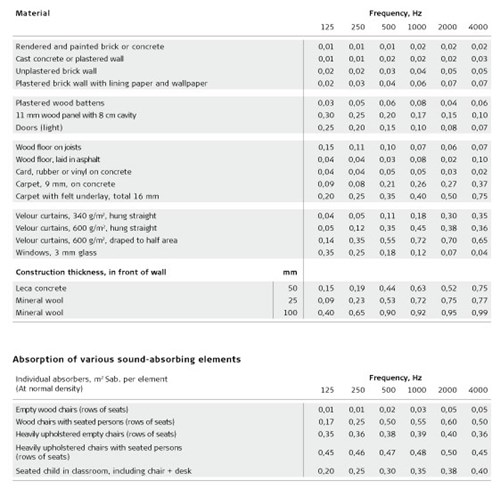
Detta sker i form av data för ljudabsorptionskoefficienten (α) (se t.ex. tabellen på sida 9). Eftersom den ljudabsorberande effekten för materialen är frekvensberoende, återspeglas detta i α-värden för de olika frekvenserna, normalt i frekvensområdet 125-4 000 Hz.
Det är oftast möjligt att få α-värden för de olika materialen från de enskilda tillverkarnas webbplatser (se www.troldtekt.com, till exempel). I handböcker och på internet är det möjligt att hitta data för byggmaterial som inte är avsedda som akustikmaterial, som golv, fönster, murverk och så vidare. Tabellen på nästa sida kan också användas som utgångspunkt. Som ses är beräkningen linjär; med andra ord adderas bidraget från de olika materialen och byggelement till absorptionen för att ge oss den totala absorptionen (A), som ingår i Sabines ekvation. För ett givet rum görs beräkningen individuellt för varje frekvensband. Detta ger oss efterklangstiden i rummet för varje frekvensband och därför efterklangskurvan för rummet. Efterklangskurvan är efterklangstidens frekvensberoende för rummet i fråga. Formen på efterklangskurvan uttrycker den akustiska kvaliteten för rummet i fråga. Men vi kommer att återkomma till detta senare.
Figur 7:
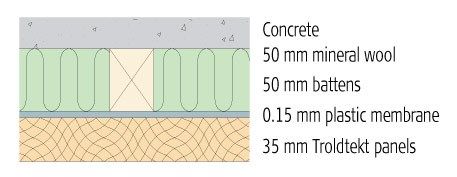
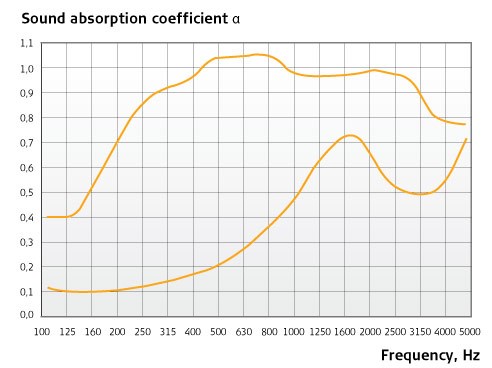
>> Läs också nästa avsnitt om olika typer av absorption